Find the Fourier series of f (x)= x^3 in x = Π to Π Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up next In order to find for any function f(x), we must apply the 'transformation' y=x In order to do that, we must define x in terms of y, ie, find f(y), then set y=x Let y=f(x) y=(x3)^31 y1=(x3)^3 x3=root(3)(y1) x=3root(3)(y1) We've now found f(y), so we must set y=x by replacing x with y and y with x f^1(x)=y=3root(3)(x1) Explanation First of all, let's compute the derivative of f (x), indicated as f '(x) f (x) = − x3 −3 ⇒ f '(x) = −3x2 In fact, to derive a sum you must derive each single term The first term is a power of x, and the derivative of xn is nxn−1 So, the derivative of x3 is 3x3−1 = 3x2, and since we had a minus sign in front of it, we will have to change signs the derivative of −x3 is −3x3−1 = −3x2

Verifying Inverse Functions By Composition Not Inverse Video Khan Academy
F(x)=x^3 is one one or onto
F(x)=x^3 is one one or onto- Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?Replace the variable x x with 3 3 in the expression f ( 3) = − ( ( 3) − 3) 3 2 f ( 3) = ( ( 3) 3) 3 2 Simplify the result Tap for more steps Simplify each term Tap for more steps Subtract 3 3 from 3 3 f ( 3) = − 0 3 2 f ( 3) = 0 3 2 Raising 0 0 to any positive power yields 0 0




Funcion F X X 3 Youtube
Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations context This looks much worse thanGraph f (x)=x^3 f (x) = x3 f ( x) = x 3 Find the point at x = −2 x = 2 Tap for more steps Replace the variable x x with − 2 2 in the expression f ( − 2) = ( − 2) 3 f ( 2) = ( 2) 3 Simplify the result Tap for more steps Raise − 2 2 to the power of 3 3 The function f(x) is continuous at point a if and only if the limit lim_(x>a) f(x) exists and equals f(a) So to prove that a function is continuous first you have to calculate the limit lim_(x>1) (x2x^3)^4=(1(1)^3)^4=(2)^4=16 The limit exists, so now you have to calculate f(1) and check if the value equals the limit f(1)=(1(1)^3)^4=(2)^4=16 The calculation shows, that f(
X!af(x), we can derive many general laws of limits, that help us to calculate limits quickly and easily The following rules apply to any functions f(x) and g(x) and also apply to left and right sided limits Suppose that cis a constant and the limits lim x!a f(x) and lim x!a g(x) exist (meaning they are nite numbers) Then 1lim x!af(x) g(xA teacher at a secondary school in London reviews equations on a whiteboard Credit Peter Macdiarmid, via GettyShort Solution Steps f ( x ) = x ( 1 \frac { 4 } { x 3 } ) f ( x) = x ( 1 − x 3 4 ) To add or subtract expressions, expand them to make their denominators the same Multiply 1 times \frac {x3} {x3} To add or subtract expressions, expand them to make their denominators the same
− x − 3 (x − 3) = 1;Solution for f(x)=x^39 equation Simplifying f(x) = x 3 9 Multiply f * x fx = x 3 9 Reorder the terms fx = 9 x 3 Solving fx = 9 x 3 Solving for variable 'f' Move all terms containing f to the left, all other terms to the right Divide each side by 'x' f = 9x1 x 2 Simplifying f = 9x1 x 2F ( x) = 3 x 3 − x 2 By Rational Root Theorem, all rational roots of a polynomial are in the form \frac {p} {q}, where p divides the constant term 2 and q divides the leading coefficient 3 One such root is 1 Factor the polynomial by dividing it by x1 Polynomial 3x^ {2}3x2 is not factored since it does not have any rational roots
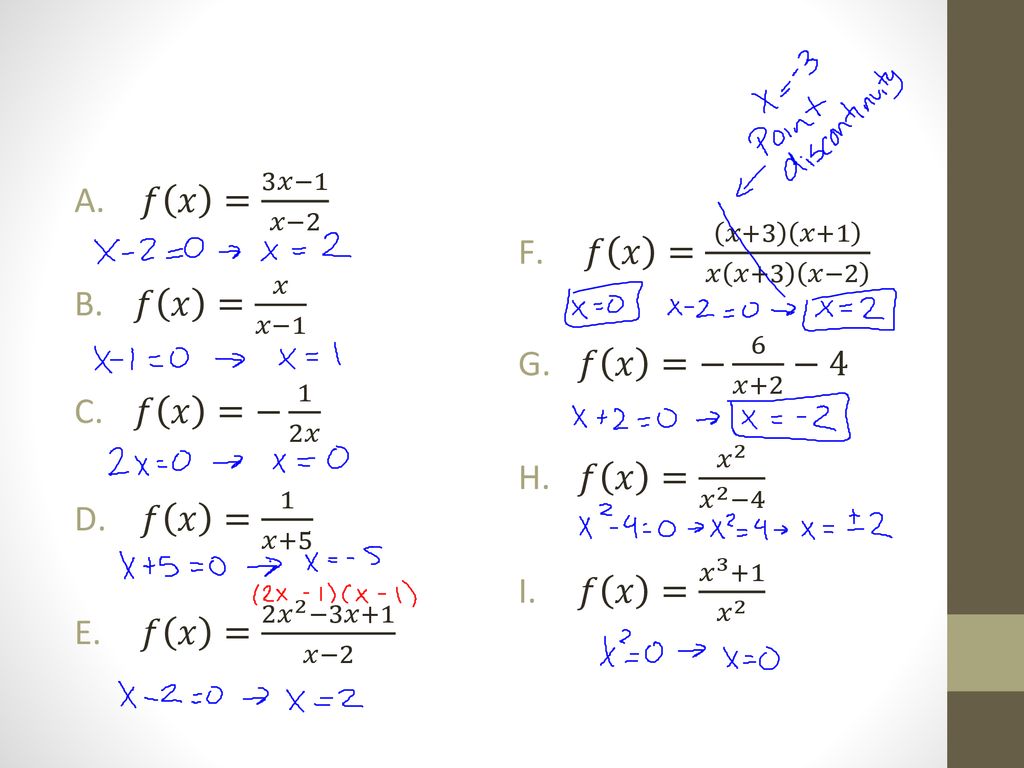



3 7 Graph Of Rational Functions Ppt Download
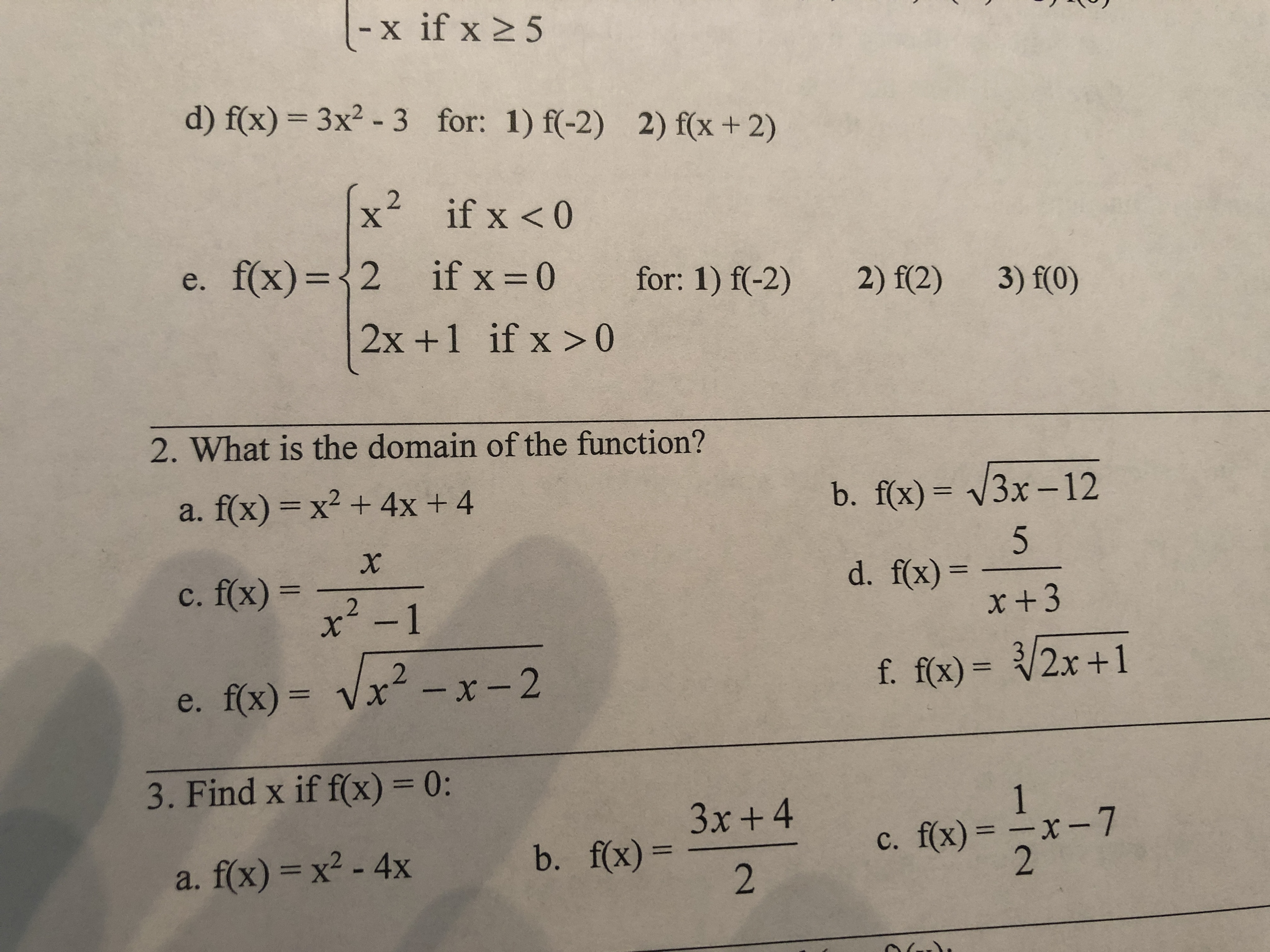



Answered X If X 2 5 D F X 3x2 3 For 1 F 2 Bartleby
Since f(−x) = e− (− x) 2 2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞) • Atx = 0, f 0(x) = 0 Thus f(0) = e = 1 is the (only) local andF (x) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ (x − 3) (x − 3) = 1;Mathf(x)=x/math Function is giving the absolute value of mathx/math whether mathx/math is positive or negative See the y axis of graph which is mathf(x)/math against mathx/math, as x axis It shows y axis values or mathf(x




Mcq Class 12 If F X 3 X 3 1 3 Then Fof X Is Teachoo




Ex 1 3 4 If F X 4x 3 6x 4 Show That Fof X X
x inRR,x!=3 y inRR,y!=0 >"the denominator of "f(x)" cannot be zero as this" "would make "f(x)" undefined Equating the " "denominator to zero and solving gives the value" "that x cannot be" "solve "x3=0rArrx=3larrcolor(red)"excluded value" "domain is "x inRR,x!=3 (oo,3)uu(3,oo)larrcolor(blue)"in interval notation" "to find the range, rearrange making x the subject" f(x)=y=1/(x3) rArry(x3Since `lim_ (x>c)f (x)=f (c)` f is continuous at all positive real numbers Therefore, f is continuous function We will now show that f (x)=x3,x in R is not differentiable at x = 3 `lim_ (h>0^) (f (3h)f (3))/h=lim_ (h>0^) (3h333)/h=lim_ (h>0^) (h0)/h=lim_ (h>0^)h/h=1`Justify your answer f (x) = ((x − 2)/(x − 3)) Check oneone f (x1) = ((x"1 " − 2)/(x"1" − 3)) f (x2) = ((x"2 " − 2)/(x"2" − 3)) Putting f (x1) =



Solution Find The Maximum Or Minimum Value Of The Function F X X 2 3 2x 7 X 2 2 1 3 2 2 3 2 1 3 2 3 Maximum X 2 6x 21 3 X 2 6x 9 21 9 3
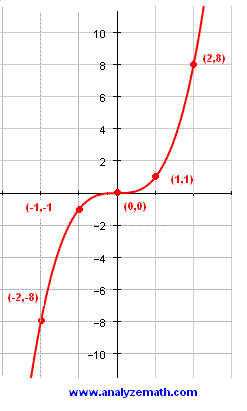



Graphing Cubic Functions
Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the first Any x value that makes any denominator in the function equal to 0 is a point of discontinuity So for the function above, x − 3 = 0 when x = 3, and so the function will be discontinuous at x = 3 The only exception to this is if the function is piecewise defined at potential "breaking" points, like this f ⋆(x) = { x2−9 x−3, x ≠ 3 6F (x)=x^3 f (x)=\ln (x5) f (x)=\frac {1} {x^2} y=\frac {x} {x^26x8} f (x)=\sqrt {x3} f (x)=\cos (2x5) f (x)=\sin (3x) functionscalculator f\left (x\right)=x^3
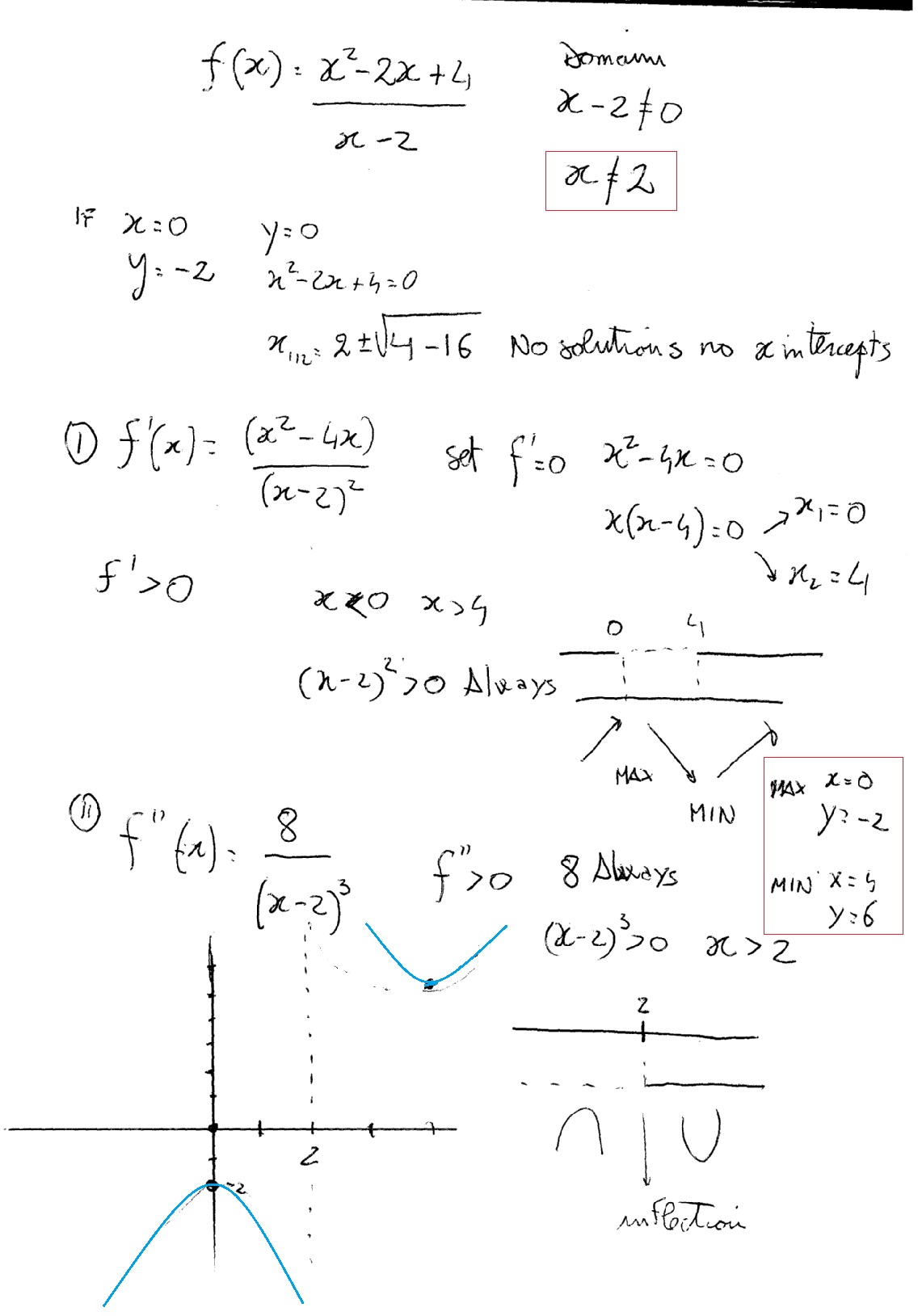



F X X 2 2x 4 X 2 F X X 2 4x X 2 2 F X 8 X 2 3 How To Find The Domain Of F X X And Y Intercepts Vertical Asymptotes The Critical Numbers Concave Up And Down And Sketch Graph Socratic



Biomath Functions
For example, we can subtract the functions f(x) = √x and g(x) = x − 8 as, The domain of the ( f − g )( x ) consists of all x values that are in the domain of both f and g In this case, f has domain {x x ≥ 0}, and g has domain all real numbers, therefore ( f − g )( x ) has domain {x x ≥ 0}, because these values of x are in theGraph f (x)=x3 f (x) = x − 3 f ( x) = x 3 Rewrite the function as an equation y = x− 3 y = x 3 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x∴ f(x) = x 3 6x 2 11x 6 As f(x) is a polynomial in x (1) f(x) is continuous on 0, 4 (2) f(x) is differentiable on (0, 4) Thus, all the conditions of LMVT are satisfied To verify LMVT we have to find c ∈ (0,4) such that




41 Find The Inverse Function For F X 3 X 7 Youtube



Search Q X 3d3 Graph Tbm Isch
Graph f (x)=3^x f (x) = 3x f ( x) = 3 x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 03 Find the indicated derivative for each function Show your work (Sec 26) Find y000, y= 4x4 x2 7 Solution y0= 16x3 2x y00= 48x2 2 y000= 96x Find d2f dx2, where f(x) = xsinx Solution f0(x) = xcosx sinx f00(x) = cosx xsinx cosx= 2cosx xsinx Find r(4), where r(x) = 1=x Solution r0(x) = 1=x2 r00(x) = 2=x3 r000(x) = 6=x4 r(4)(x) = 24=x5 4 Find a tangent line through the curve 2x 2Free tangent line calculator find the equation of the tangent line given a point or the intercept stepbystep




Differentiation F X X 3 2x 2 3x 5 F X 3x 2 4x 3 F 1 3 X X 1 3 3 4 If F X X 3 2x 2 Ppt Download



How To Graph Parent Functions Dummies
F (x)=x^3 prove\\tan^2 (x)\sin^2 (x)=\tan^2 (x)\sin^2 (x) \frac {d} {dx} (\frac {3x9} {2x}) (\sin^2 (\theta))' \sin (1) \lim _ {x\to 0} (x\ln (x)) \int e^x\cos (x)dx \int_ {0}^ {\pi}\sin (x)dx \sum_ {n=0}^ {\infty}\frac {3} {2^n}Example f R ⇥ R where f(x) = x2 is not onetoone because 3 ⌅= 3 and yet f(3) = f(3) since f(3) and f(3) both equal 9 Horizontal line test If a horizontal line intersects the graph of f(x) in more than one point, then f(x) is not onetoone The reason f(x) would not be onetoone is that the graph would containConsider x^ {2}4x3 Factor the expression by grouping First, the expression needs to be rewritten as x^ {2}axbx3 To find a and b, set up a system to be solved a=3 b=1 Since ab is positive, a and b have the same sign Since ab is negative, a and b are both negative The only such pair is the system solution




Verifying Inverse Functions By Composition Not Inverse Video Khan Academy




Evaluate Functions For X Given F X 3 Youtube
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music Misc 7 Find the intervals in which the function f given by f (x) = x3 1/𝑥^3 , 𝑥 ≠ 0 is (i) increasing (ii) decreasing f(𝑥) = 𝑥3 1/𝑥3 Finding f'(𝒙) f'(𝑥) = 𝑑/𝑑𝑥 (𝑥^3𝑥^(−3) )^ = 3𝑥2 (−3)^(−3 − 1) = 3𝑥2 – 3𝑥^(−4) = 3𝑥^2−3/𝑥^4 = 3(𝑥^2−1/𝑥^4 ) Putting f'(𝒙) = 0 3(𝑥^2−(a) Find the average value of on the given interval (b) Find such that (c) Sketch the graph of and a rectangle whose area is the same as the area under th




Let F X X 2 3 4 X 2 3 3 X 4 5 Then D Dx Chegg Com
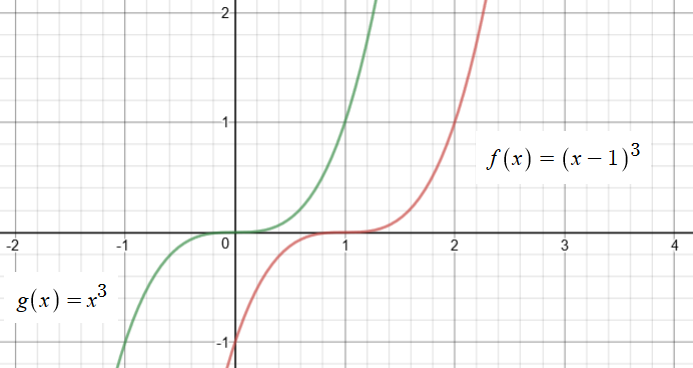



What Is The Equation Of The Tangent Line Of F X X 1 3 At X 2 Socratic
F ( x) = x2 A function transformation takes whatever is the basic function f (x) and then "transforms" it (or "translates" it), which is a fancy way of saying that you change the formula a bit and thereby move the graph around For instance, the graph for y = x2 3 looks like this This is three units higher than the basic quadratic, f (x) = x2F (x) = 3x − 3 f (x) = 3 x 3 Rewrite the function as an equation y = 3x− 3 y = 3 x 3 Use the slopeintercept form to find the slope and yinterceptFind f (–1) " (pronounced as " f of x equals 2 x plus three;




Find The Domain And The Range Of The Real Function F X 1 X 3




Answered Express The Function In The Form F G 1 Bartleby
Math131 Calculus I The Limit Laws Notes 23 I The Limit Laws Assumptions c is a constant and f x lim ( ) →x a and g x lim ( ) →x a exist Direct Substitution Property If f is a polynomial or rational function and a is in the domain of f, then = f x lim ( ) x aSimple and best practice solution for f(x)=3x3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,H(x) = 3(x 2 8x 16) = 3(x 4) 2 = 3 ∙ f(x 4) From this factored form, we can see that h(x) is the result when f(x) is translated 4 units to the left and stretched vertically by 3 Take note of the factor multiplied to √x and the unit subtracted from the input value




Funcion F X X 3 Youtube
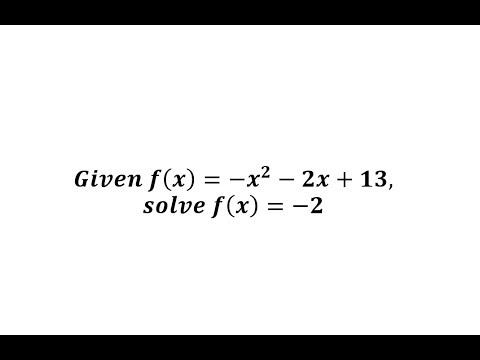



Given F X X 2 2x 13 Solve F X 2 By Factoring Youtube
So, f(x) is continuous at x=3 RHD of f(x) at x=3 , lim h → 0 { 3 h − 3 ( 3 h ) − 3 − ( 3 − 3 ) } = 1 LHD of f(x) at x=3 , lim h → 0 { 3 − h − 3 3 − ( 3 − h ) − ( 3 − 3 ) } = − 1You used to say "y = 2x 3;Solve for y when x = –1" Now you say " f ( x ) = 2 x 3 ;




Domain And Range Of F X X 3 X 3 Are Respectively



Show That The Function F X X 3 X R Is Continuous But Not Differentiable At X 3 Sarthaks Econnect Largest Online Education Community
Short Solution Steps f ( x ) = x ^ { 3 } ( 1 \frac { 4 } { x 6 } ) f (x) = x3(1 − x 64 ) To add or subtract expressions, expand them to make their denominators the same Multiply 1 times \frac {x6} {x6} To add or subtract expressions, expand them to make their denominators the sameR > 0 then the function de–ned by f (x) = X1 n=0 c n (x a) n = c 0 c 1 (x a) c 2 (x a) 2 is di⁄erentiable (hence) continuous on (a R;aR) and 1 f0 (x) = c 1 2c 2 (x a)3c 3 (x a) 2 In other words, the series can be di⁄erentiated term by term 2 R f (x)dx = C c 0 (x a)c 1 (x a)2 2 c 2 (x a)3 3 In other words, theFind f ofnegativeone") In either notation, you do exactly the same thing you plug –1 in for x , multiply by the 2 , and then add in the 3 , simplifying to get a final value of 1
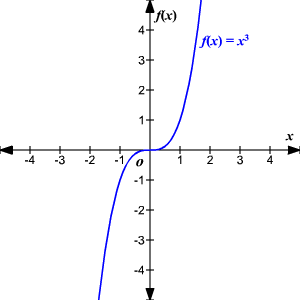



Even Odd Functions




What Is The Difference Between F X X 2 1 And F X X 3 1 When Finding The Inverse Mathematics Stack Exchange
To find the value of a function, f (x), simply put the value of x (this problem has x=3) into the expression For example, if f (x) = 2x 7 then f (3) = 2 (3) 7 f (3) = 1 Upvote • 2 Downvote Add comment MoreFind the domain of the composite function f of g Like the Function f (x)=x^3 Tom McCoy returns to bamboozle us And over what?




Example 8 Show F X X3 3x2 4x Is Strictly Increasing



More Differentiation By First Principles
The function f(x) = x3 is increasing between 0 and 1 Therefore the supremum of the values on an interval (x i 1;x i) is f(x i) = x3i, and the in mum is f(x i 1) = x3i 1 Thus we can calculate the lower and upper sums of fwith respect to D n L(f;D n) = i=1 (i 1 n)3 1 n = 1 n4 i=1 (i 1)3 = 1 4n4 (n4 2n3 n2) n3 n4 = 1 4 1 2n 1 4n2 AX > 3 x < 3Hence the slope of the graph of the square function at the point (3, 9) is 6, and so its derivative at x = 3 is f ′ (3) = 6 More generally, a similar computation shows that the derivative of the square function at x = a is f ′ (a) = 2a




Prove That The Function Given By F X X3 3x2 3x 100 Is Increasing In R Mathematics Shaalaa Com




Let F X 3 X 2 4 X 3 5 X 4 Then F X 0 Has A Exactly One Real Root In 2 3 B Exactly One Real Root In 3 4 C At Least One Real Root In 2 3 D None Of These
4 The table of values for f(x) is shown below If g(x) is the result of f(x) being horizontally stretched by a scale factor of 3, construct its table of values and retain theF − 3x2 View solution steps Steps Using Derivative Rule for Sum f ( x ) x ^ { 3 } 1 f ( x) − x 3 1 The derivative of a polynomial is the sum of the derivatives of its terms The derivative of a constant term is 0 The derivative of ax^ {n} is nax^ {n1} The derivative of a polynomial is the sum of the derivatives of its termsSolution for f (x)=3 equation Simplifying f (x) = 3 Multiply f * x fx = 3 Solving fx = 3 Solving for variable 'f' Move all terms containing f to the left, all other terms to the right Divide each side by 'x' f = 3x 1 Simplifying f = 3x 1




If F X X 1 X 2 X 3 Then A Maximum Value Of F X Is 3 If X In 2 3 B Maximum Youtube



What Is The Point Of Inflection Of X 3 Quora
Simple and best practice solution for F(x)=(x1)(x3) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it3 The function, f(x), passes through the point (10, 8) If f(x) is horizontally stretched by a scale factor of 5, what would be the new xcoordinate of the point?



How To Find F 2 If F X 2 5x 4 X 3 Quora



Suppose G X F X 3 4 Which Is Statement Best Compares The Graph Of G X With The Graph Of F X Mathskey Com



Sage Calculus Tutorial Continuity




If F X 1 2x 5 Find F 3 And Find F X 1 Youtube



F X X 3




Misc 5 Show F X X3 Is Injective Chapter 1 Class 12 Cbse




A Function F Is Defined By F X 3 2x Find X Such That F X F X Brainly In



F X X 3 2 3 2x 2 X 2 Geogebra




Show That The Function F X Modulus Of X 3 Is Continuous But Not Differentiable At X 3 Mathematics Topperlearning Com 8yq4x399




Example 8 Find Derivative Of F X 3 At X 0 X 3 Examples




If F X 3 X 1 X 2 3x Find F 0




Example 4 Show F X X3 3 1 Is Not Continuous At X 0



Solution Graph F X X 3 2 Include All Intercepts And The Vertex I Am Not Sure How To Do The Absolute Value Signs On Here But They Should Go Where The Parentheses Are Thank You




If F X 3 4x 5 Then Find F 5 And F X Youtube



How Do You Graph F X 3 X 2 Socratic



Mhf4u1 P1 8 2 Main




Sketch The Graph Of F X X 3 X 2 7 The Domain Is Chegg Com




Maclaurin Series For F X 1 1 X 3 Math Calculus Showme



Domain And Range



1




F X X 2 X 2 4 F X X 3 X 2 9 F X Chegg Com



1




Maximum Value Of Function F X Frac X 4 X 2 X 6 2x 3 1 When X 1 Mathematics Stack Exchange




If F X X 3 X 2 F 1 11 2 Then F X




Domains 31 F X X3 2x2 G X 3x2 1 32 F X Chegg Com
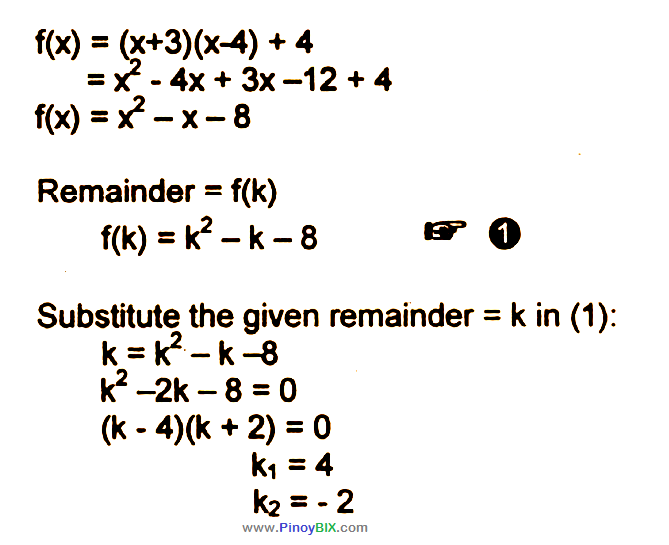



Solution Given F X X 3 X 4 4 When F X Is




Misc 18 If F X X 3 Show That F X Exists And Find It




What Is The Domain And Range Of F X Abs X 3 5 2 Socratic




The Table Represents The Function F X What Is F 3 Home Work Help Learn Cbse Forum
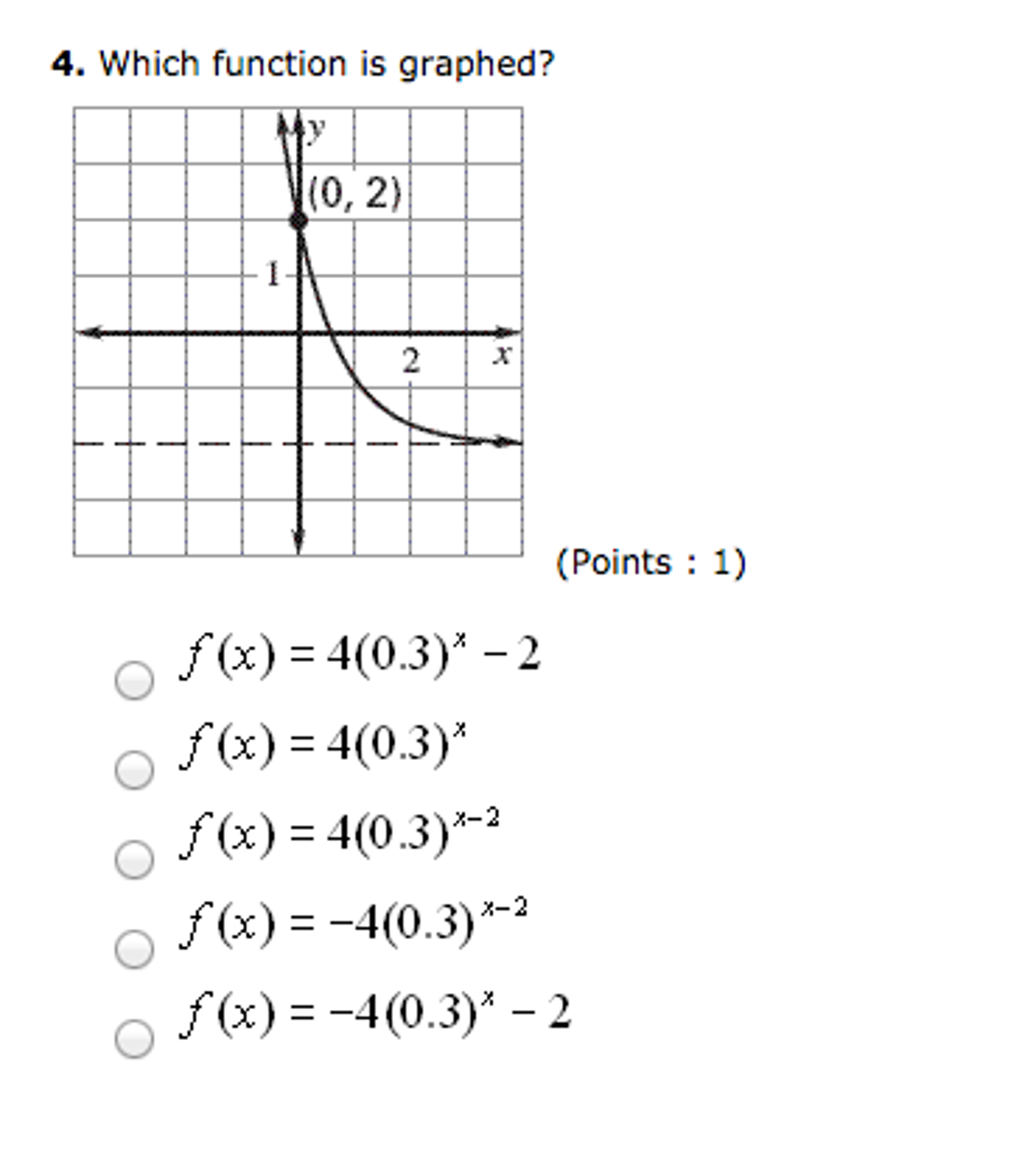



1 Find The Inverse Of The Function F X 3 5 Points Chegg Com
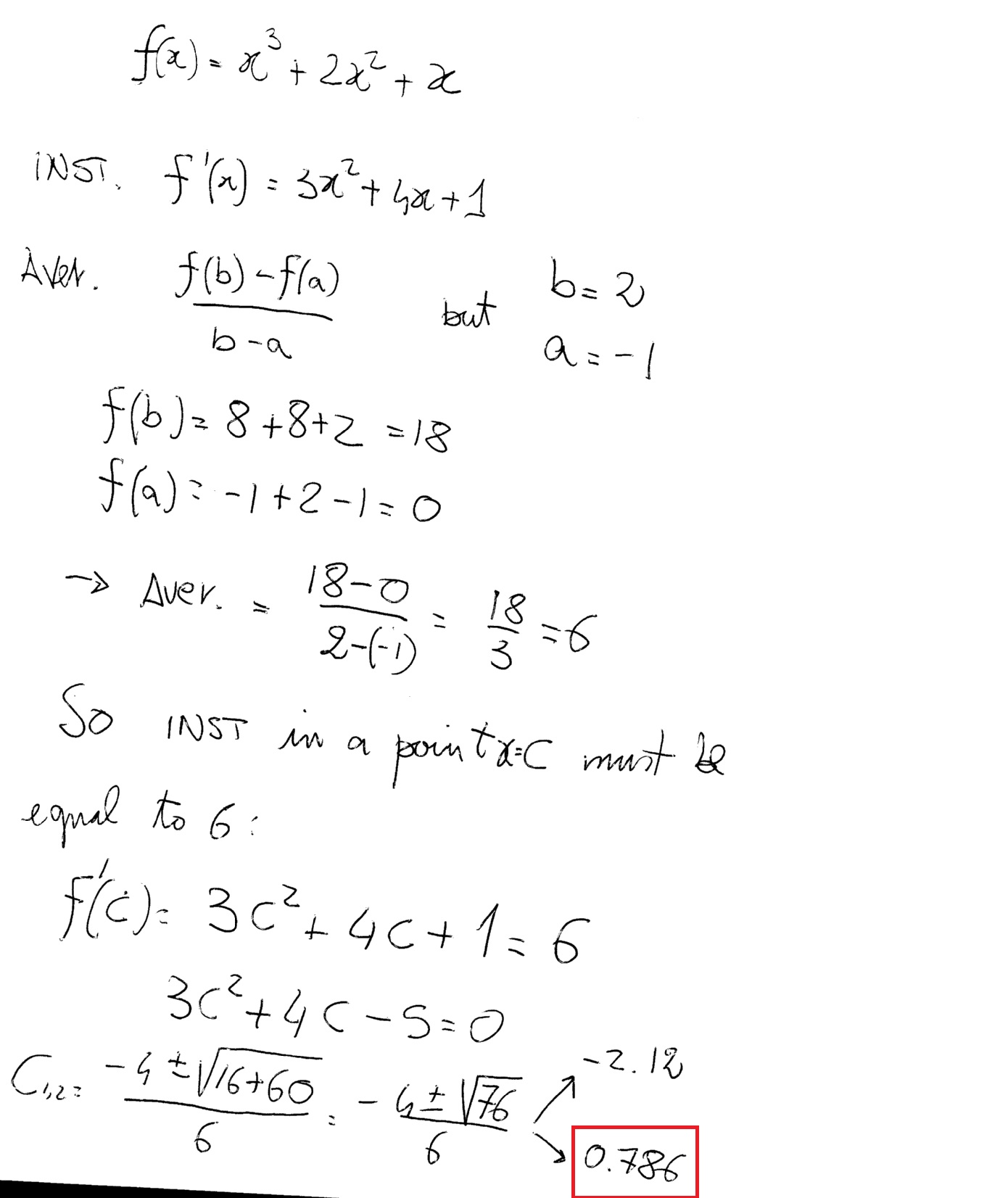



If F Is Defined By F X X 3 2x 2 X How Do You Find The Value Of X When The Average Rate Of Change Of F On The Interval X 1 To X




Given That F X 2 X 4 And G X 3 X 5 Find Gf 3 With Noob Like Steps Please I Need A Really Clear Working To Fully Understand Thanks 3 Socratic




F X X 3 2 And G X 2x 3 Find Fog And Gof Is F Inverse G Maths Relations And Functions Meritnation Com
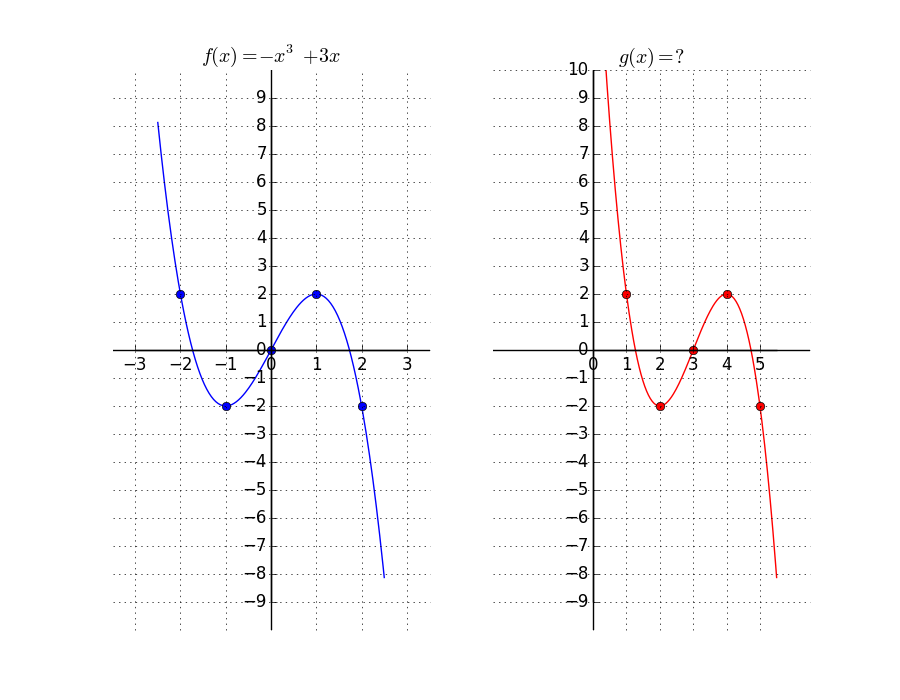



Given The Graph Of The Function F X X3 3x Find Chegg Com



The Function F X X 3 X 1 F X X 2 4 3x 2 13 4 X 1 Is Sarthaks Econnect Largest Online Education Community




If F X X3 1 X3 Prove That F X F 1 X 0 Brainly In




Show That Function F In A R 2 3 Defined As F X 4x 3 6x 4 Is One One And Onto Hence Find F 1 Mention Each And Every Formula And Minute Details Mathematics Topperlearning Com W22iulbb




How To Find The Domain Of F X X 1 X 2 X 3 X 4 Quora
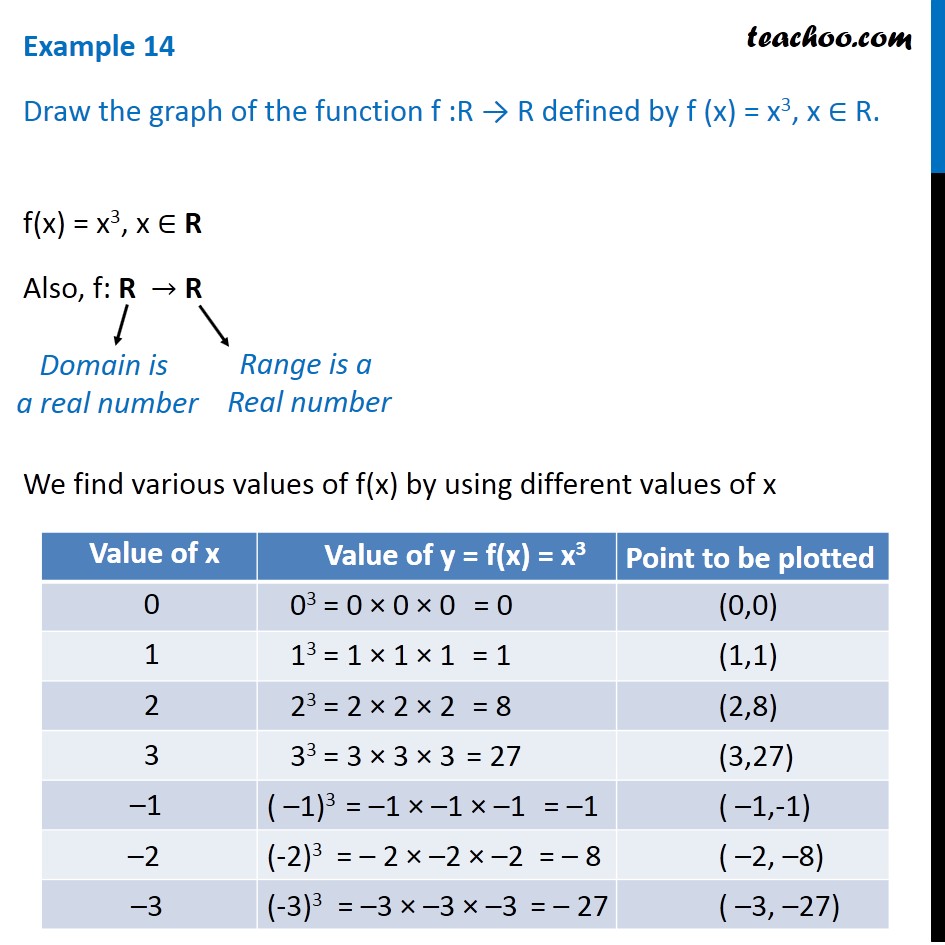



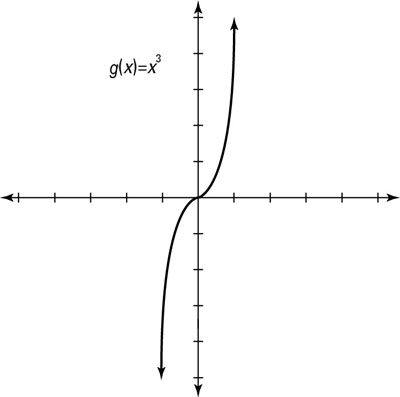
Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11
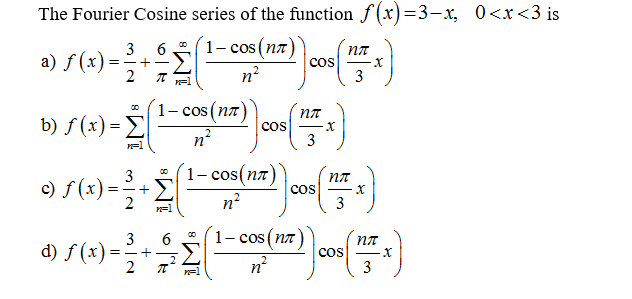



The Fourier Cosine Series Of The Function F X 3 X Chegg Com



What Are The Domain And Range Of The Function F X 3 X 5 Solved
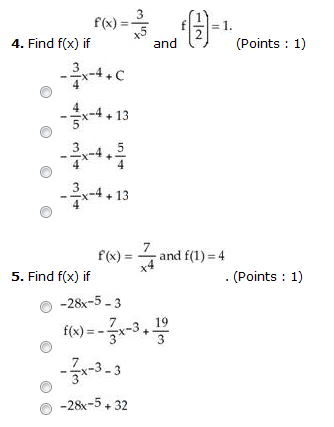



Find F X If F X 3 X5 And F 1 2 1 3 4x 4 C Chegg Com




Find The Inverse Function Of F X X3 3 0 X Chegg Com



Prove That F X X 2 X 6 X 3 When X 3 5 When X 3 Is Continuous At X 3 Sarthaks Econnect Largest Online Education Community



F X F X 2 F X 2
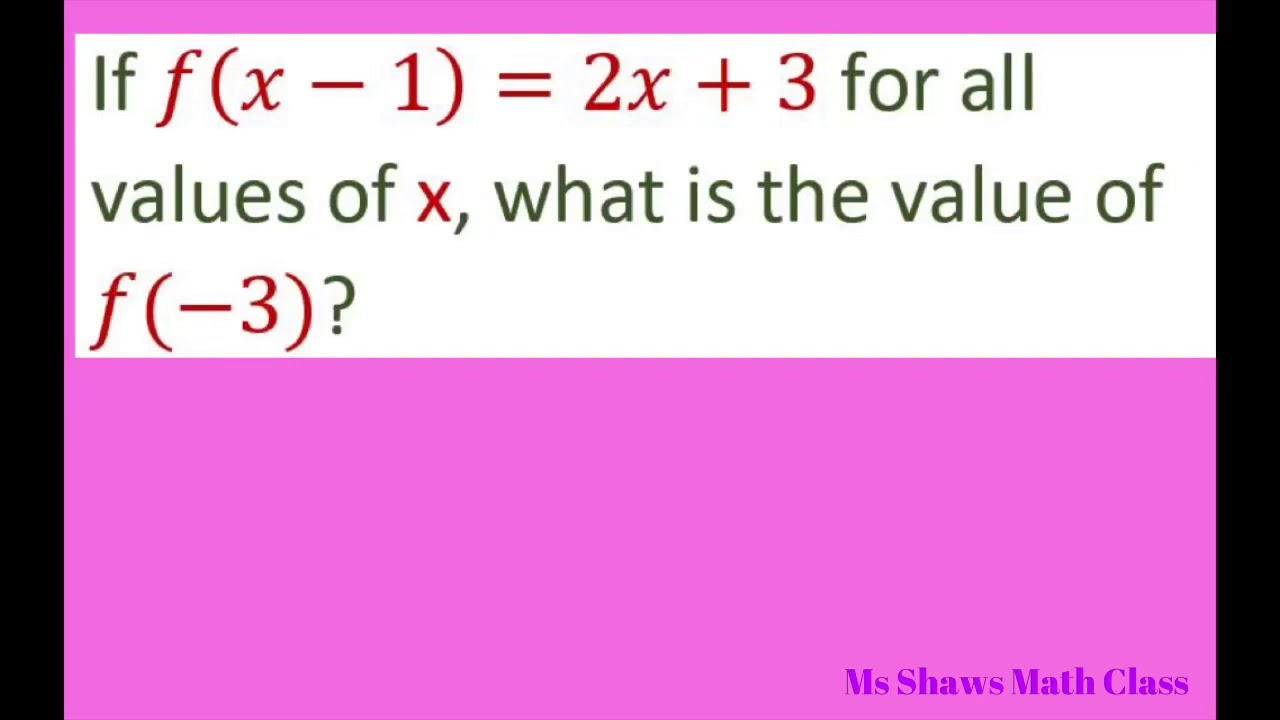



If F X 1 2x 3 Find F 3 Youtube
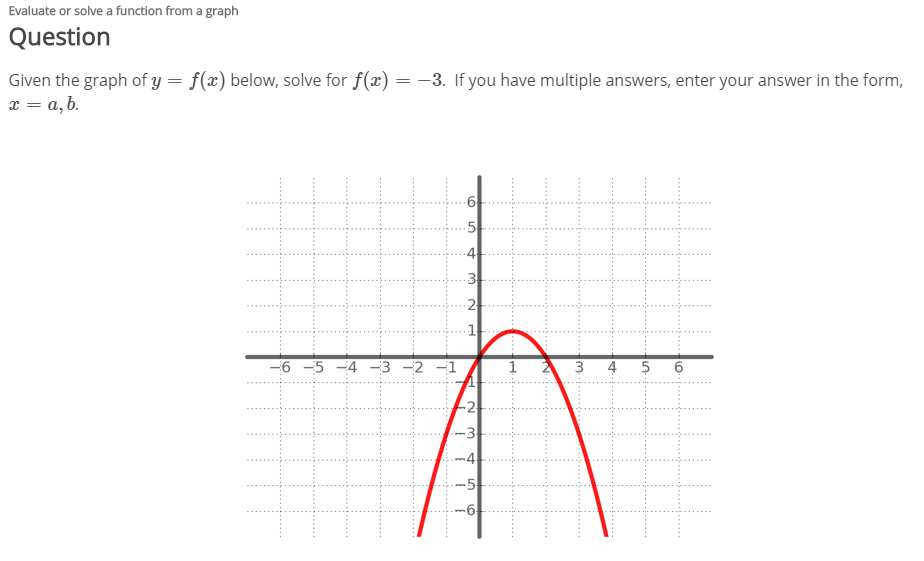



Given The Graph Of Y F X Below Solve For F X 3 Chegg Com




Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing
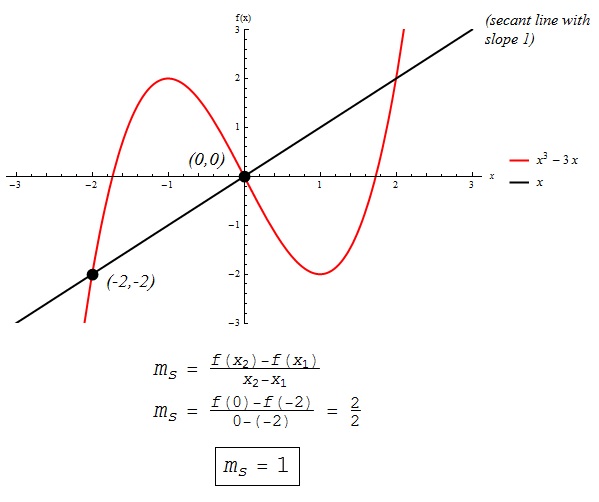



Find The Average Rate Of Change Of F X X 3 3x From X1 2 To X2 0 Enotes Com
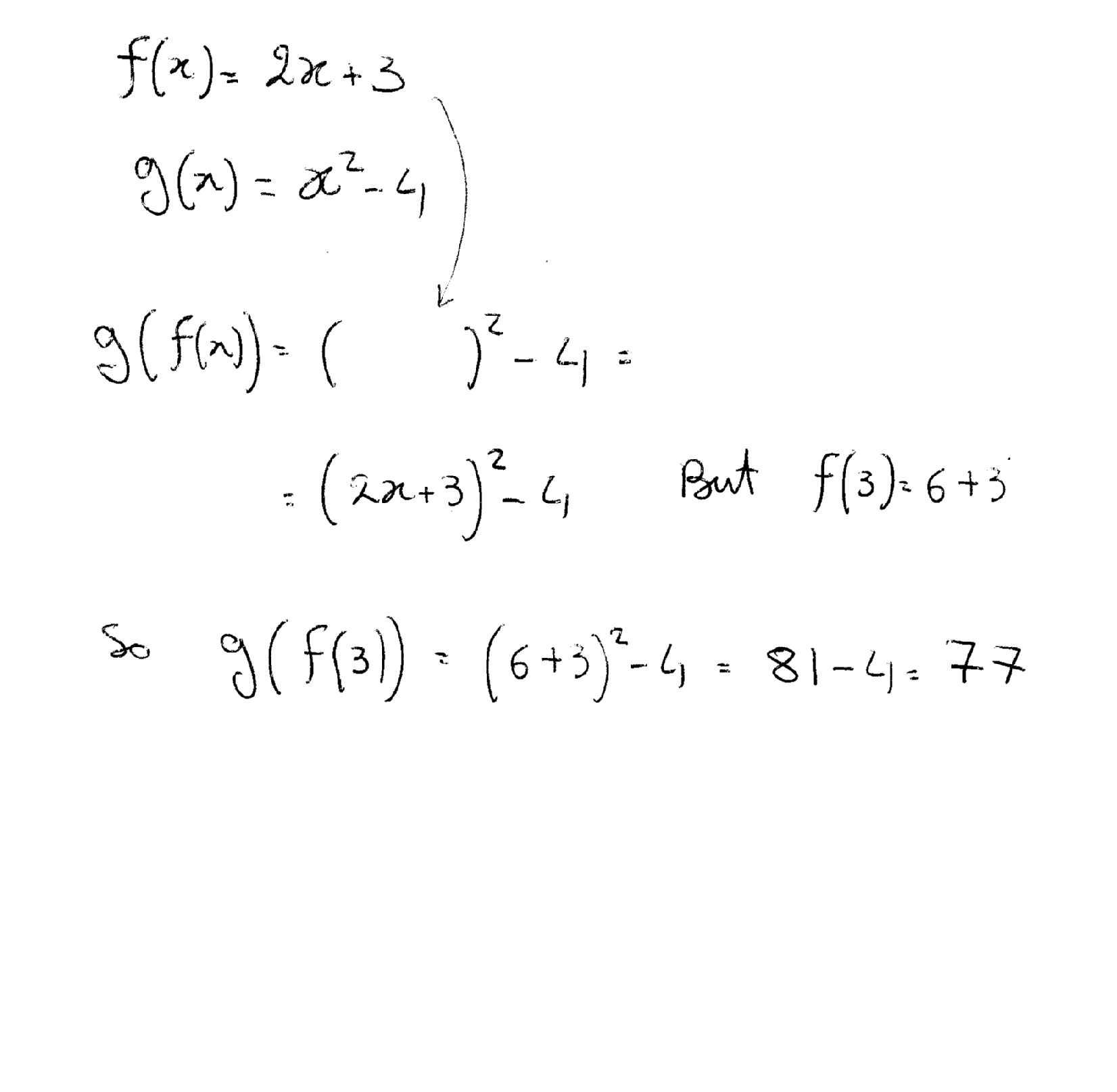



Let F X 2x 3 And G X X 2 4 And H X X 3 2 How Do You Find G F 3 Socratic




Consider The Function F X X 3 Draw The Graph Of F X Maths Relations And Functions Meritnation Com




If F X X 3 Then F 3 Is




How Do You Find F X Using The Limit Definition Given F X X 2 1 2x 3 Socratic
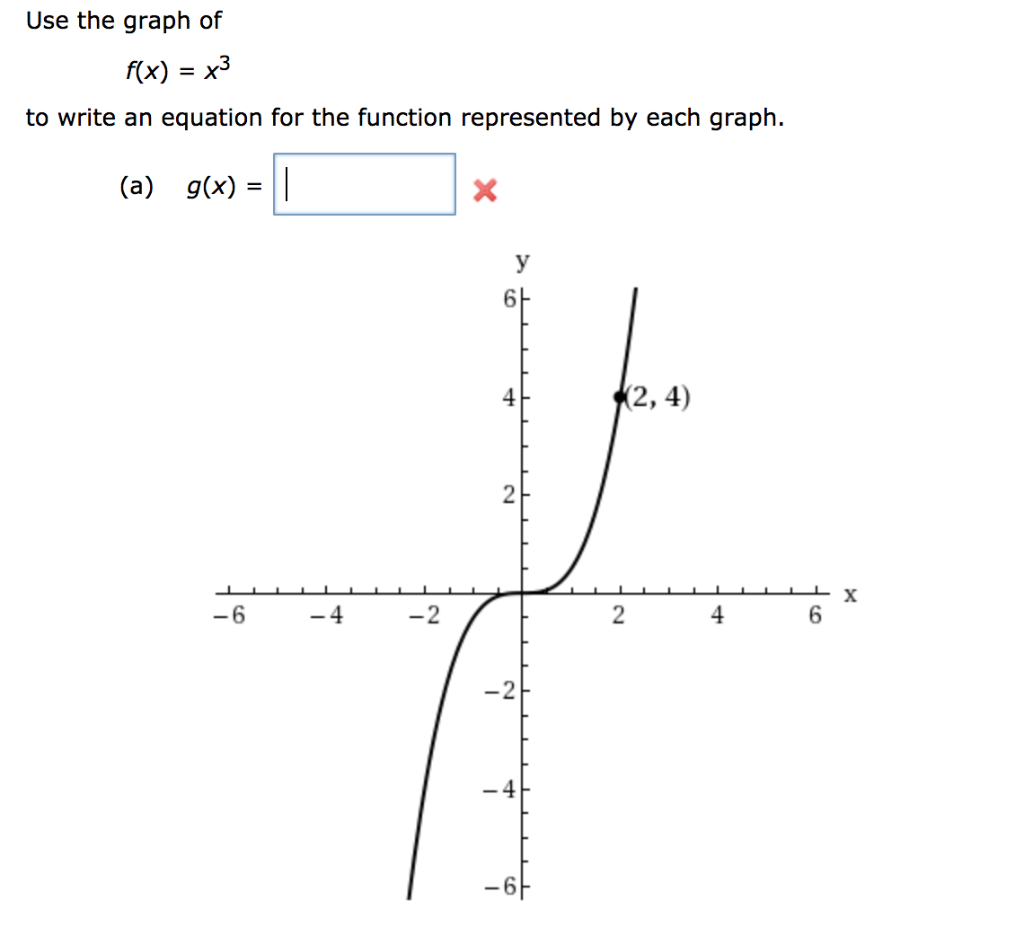



Use The Graph Of F X X3 Equation For The Chegg Com



1 The Figure Above Shows The Graph Of F X X 3 Chegg Com



Draw The Graph Of The Function F R R Defined By F X X 3 Find Its Domain And Range Sarthaks Econnect Largest Online Education Community




If F X X 2 2 And G X 2x 2 X 3 Find F G X Brainly Com



Math Scene Equations Iii Lesson 3 Quadratic Equations




19 Find The Inverse Function For F X X 3 4 Youtube
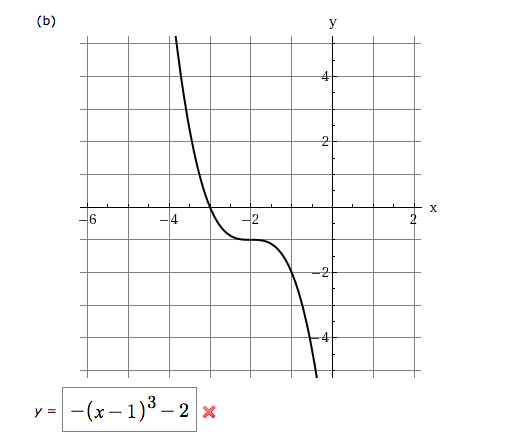



Use The Graph Of F X X3 To Write An Equation For Chegg Com
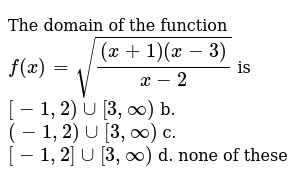



The Domain Of The Function F X Sqrt X 1 X 3 X 2 Is 1 2 Uu 3 Oo B 1 2 Uu 3 Oo C 1 2 Uu 3 Oo D None Of These




If F X X 3 Find The Value Of F 5 F 1 5 1



Solved 9 Find An If The Function F X X X3 A Finite Value B Infinite Value C Zero D Can T Be Found View Answer Course Hero



Www3 Nd Edu Apilking Math Work Old exams Exam1f08soluutions Pdf



Can You Sketch The Graph Of F X 2x 2 X 3 2x 3 And Give Its Domain Intercepts Asymptotes And Range Quora



F X F X 2 F X 2




For The Function Defined By F X X 2 X Less Than Equal To 1 2x 1 X Greater Than 1 Define F 0 And Also Draw The Graph For F X Study Com




How Do You Find The Derivative Of F X 3 X 2 Using The Limit Definition Socratic




Example 8 Discuss Continuity Of F X X3 X2 1 Examples
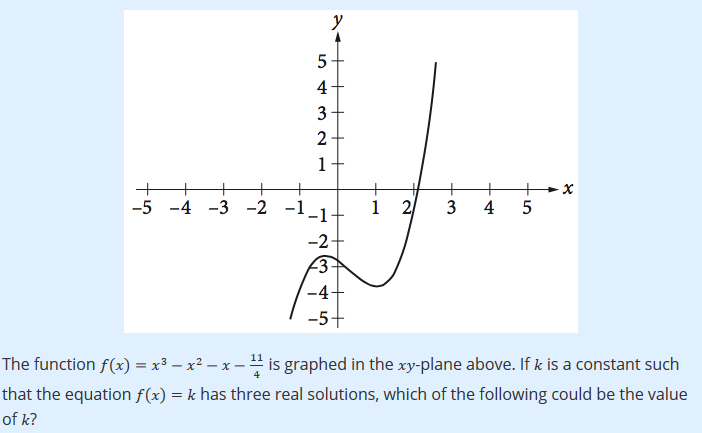



4 2 4 The Function F X X3 X2 X 11 Is Graphed In Chegg Com




Let F X X 3 X 1 And Let G X Be Its Inverse Function Then Equation Of The Tangent To Y G X At X 3 Is




The Graph Of F X X 5 5x 4 6x 3 3x 2 7x 2 Represents The Download Scientific Diagram



Transformations Mrs F X




Let F X X 3 3 A 7 X 2 3 A 2 9 X 1 If F X Has Positive Point Of Maxima Then Find Possible Values Of A



0 件のコメント:
コメントを投稿